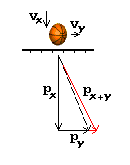Tom Jonard's Special Relativity Page

 Relative Motion | The Speed of Light Constant | Time Dilation | Simultaneity | Length Contraction
Mass Inflation | Mass and Energy | Spacetime Diagrams |  Bottom

The Special Theory of Relativity (SR) makes the following predictions:

  • Time, space and mass are not absolute:
  • The rate of a moving clock decreases as its speed increases.
  • An object contracts in the direction of its apparent motion as its speed increases.
  • The mass of an object increases as its apparent speed increases.
  • Events that appear simultaneous to one observer may not to another.
  • Mass and energy are equivalent.
  • Observations are relative to their frame of reference.
    • Scientific theories are created because there is an observation to be explained or a problem to be solved.  In the case of SR the problem if not the observation can be easily understood through thought experiments and a little mathematics.  The following discussion is my attempt to convey not just what Relativity says but also why.  This discussion will hopefully show why Relativity is an inescapable conclusion.

    Relative Motion

    Imagine that we are standing on a railroad platform as a train goes passes.  On the train is a boy dribbling a basket ball:

    How fast is the ball moving?  To find the answer we and the boy time the interval between when the ball leaves the his hand and when it returns.  We both get the same time.  We both divide the distance by the time to get feet per second.  We will ignore that the motion is not uniform, the average speed will do.  Surprisingly we both get different answers!  Why?  Because to us the ball has traveled a greater distance -- it moved down the track with the train and not just straight up and down -- its diagonal path was longer than the straight up and down path the boy will see:

    Because our frames of reference differ -- they were moving with respect to each other -- we and the boy differ about the speed of the ball.

    So far so good.  We can still convince ourselves that if only both we on the platform and the boy on the train understand what we are talking about we can come to an agreement about the true speed of the ball.  We just have to decide on whose frame of reference to use when talking about events.  Because the platform is stationary with respect to most of the rest of the world we tend to think that this is a special, privileged frame of reference and that all other motion should be transformed to reference this frame.

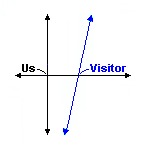
    But wait a minute!  Suppose the boy on the train objects to this!  From his perspective it is we on the platform who move in the opposite direction and at the same speed that we see the train move.  What is wrong with this?  Nothing other than that most of the rest of the world participates in our motion but not his train.  But remove the rest of the world and just considered the platform and the train.  Is there still a reason to choose one over the other as a privileged frame of reference?  The situation is equivalent to two trains passing each other so instead of a platform let us assume that we are on a train too.  Also assume that either one or both trains may be moving (at a uniform speed) and that we are in a tunnel so that we can see no external clues as to who is going how fast or even which direction.

    And now if there is also a boy on each train dribbling a basket ball each will say the other's ball is moving faster than the ball's owner says it is.  And there is no way of saying that one is right and the other wrong.  We can still transform our observations from one frame of reference to the other, but we no longer have a reason for believing or method of deciding that one frame is more privileged than the other.  We can therefore also transform our observations to any other arbitrary frame of reference.  This is the world view of classical physics until the time of Einstein.

    The Speed of Light Constant

    Let's modify our thought experiment yet again.  Instead of a dribbled basket ball let's substitute a beam of light that is bouncing between two mirrors on both trains:

     We can actually imagine these mirrors oriented in any direction and get the same result, but for the sake of analogy with what we discussed before, assume one mirror is on the floor of the train and one is on the ceiling.  What is the speed of the light beam bouncing between the two mirrors measured with this setup?  Einstein said it must be the same for both observers on both trains.  Note that this is different than the conclusion we arrived at before.  We were wrong even though there was nothing wrong with our analysis according to pre-Einsteinian physics.  Here is why:

    If it were not so observers on the other train must see light move more slowly than we do since we observe that their light has farther to go:

    But Einstein said that this does not happen.  He carried our thought experiment one step further and asked what would happen if the train could move at the Speed of Light.  According to pre-Einteinian physics observers on the train would then see light stop!  But this is not theoretically possible (light is an electro-magnetic oscillation and if it could stop it would be an electromagnetic oscillation at rest -- which is impossible) and it is also never observed (neither is any slow down in light ever observered).  The only other logical possibility is that light is always observed to move at the Speed of Light regardless of the observer's motion.

    There was experimental evidence that it the observed speed of light does not change with motion before Einstein.  The Earth rotates on its axis once a day so the velocity of a person at the equator is 1,000 mph.  It revolves around the Sun once a year carrying us all along at 66,000 mph.  The Sun revolves around the Milky Way's center in some 250 million years again carrying us all along with it at about 500,000 mph.  Yet even though we are moving all the time and even though our direction of motion changes substantially and continuously,  experiment shows that the Speed of Light is always the same no matter which direction we measure it or when.  This was discovered in 1887 by two physicists -- A. A. Michelson and E. W. Morley.  Our cosmic motion does not effect the measured Speed of Light.

    Time Dilation

    If the observers on our trains are to agree on the Speed of Light that they measure, then we are led to some extraordinary conclusions.  Time must run more slowly on their train or more quickly on ours.  More generally, time in two frames of reference in unifrom motion relative to each other will not pass at the same rate.  Two "equal" time intervals -- say a second -- will not be equivalent to observers in two such frames of reference!  Why?  Because we calculate the Speed of Light by dividing the distance it travels by the elapsed time it takes.  Only if we see time on the other train travel more slowly are we able to calculate the correct Speed of Light for both frames of reference.

    And visa versa. We on our train see time on the other train pass more slowly.  They in turn see the same thing happen on ours!  Neither of us occupies a special frame of reference where we can say. "This is the way it really is".  This sounds the same as the pre-Einsteinian relativity we talked about before but it is different in one important way -- it now includes time.  Not only is there is no special place from which to view the world there is also no special time.  When we perform a transformation from one frame of reference to another we must also consider time in the calculation.  SR shows us this and how to do this.  Previously physics had thought of space and time as being separate and independent.  SR merges them into one thing -- spacetime.

    In our everyday experience we measure time with clocks.  We used to measure time by the sun but now for convenience we do it with clocks.  A clock is any mechanism with a regularly repeating state such as a pendulum, an atomic vibration or a bean of light bouncing between 2 mirrors.  When astronauts measure time in space they do it with clocks which were built on the ground and synchronized there with other clocks.  An hour in space is just an hour on one such clock.  We assume the clock is running at the same rate as a similar one on the ground.  We assume that time is the same for everyone everywhere.  SR says that this assumption is wrong.  Time is not the same everywhere.  The Speed of Light is.

    Simultaneity

    To say that we see events as simultaneous means that we receive light (or perhaps some other signal) from the events at the same time.  Suppose we wish to record some of our observations by photographing the boy with the basketball as our trains pass.  To get even lighting we sets up 2 flashes so that the scene on the other train will be evenly illuminated as it passes.  We are prepared to take the picture just as the boy passes by.

    Luckily we are able to time the flashes to go off just as the boy is half way between them.  And to us they appear to be simultaneous.  But they fail to evenly illuminate our subject.  Instead the light from the flash toward the front of the passing train reaches the boy first, trailed some time by the light from the other flash.  The flashes do not appear to be simultaneous to the boy or anyone else on the other train though they do to us.

    The above thought experiment closely follows one provided by Einstein.  A more interesting and paradoxical example is to consider what happens if the photographer and his flashes are on the train with the boy.  It can again be arranged by luck that the flashes occur just as the other train passes us so that they appear simultaneous to us.  We again conclude that they will not appear simultaneous on the other train as before.  But if we and they agree on the Speed of Light then certainly they must measure the same for the light from both flashes.  Therefore both will reach the boy at the same time and appear simultaneous to him.

    We commonly think of simultaneity as a absolute.  But as we have seen our definition of simultaneity is effected by the relative motion of our frame of reference and that of the events whose simultaneity we are trying to determine.  And there is no preferred frame of reference in which we can determine simultaneity.  Not only is the passage of time not the same for everyone everywhere as we commonly think, the relationship of events in time is not fixed but relative to our motion .

    Length Contraction

    What is the length of the car in which our basket ball player is riding?  If the car is not moving this is a simple thing to determine.  We all get out our tape measures or yardsticks and measure the car.  We no doubt agreement on the answer to this question.  And this is not surprising.  But what happens if the car is moving?  In the simplest sense we who observe the train passing can no longer just measure the car with a measuring device.  We must resort to some more indirect means of determining the length of the car.  But nevertheless we expect that in the end we will all still agree on its length.

    One method of determining the length of the car given that we know the speed at which the train is passing is to time how long it takes the car to pass.  The length of the car (l) is then given by:

    l = v t
    where v is the speed and t is the time it takes to pass.  We can just measure with a stopwatch the time between when the front of the car passes directly before us (t1) and the time when the rear of the car does the same (t2).  We then multiply the time (t2 - t1) by the speed of the train to get the length of the car.

    Of course our observers on the train can still use their tape measures or yard sticks and measure the car as they did when it was not moving.  And they will find that its length has not changed.  But what if they choose to use the same method we do -- timing how long it takes the car to pass our position?  One observer will have to be stationed at the front of the car to note the time (t1) when that part of the train passes us.  Another must be stationed at the rear to do the same and determine (t2).  One must communicate their time to the other or both to a third party somewhere else on the car -- it doesn't really matter as the result will be the same.  And the length measured in this way will be the same found by conventional tape measure & yardstick.

    So far so good.  But what do we observe from our position in relative uniform motion with respect to their car?  We already know that time is traveling slower on their train than it is for us.  So we interpret the length of the car calculated by its occupants timing its passage differently than they do.  There can be no disagreement between us all as to when the events that demarcate t1 and t2occur.  We can wave to our counterparts on the other train as the front and rear of their car passes us.  Nevertheless it appears to us that more time passes in their moving frame of reference between these two events so that the time (t2 - t1) used to calculate the length of their car appears longer as well.  We can reconcile the contradiction by assuming that their car has contracted in the direction of motion.  Note that this is a phenomenon observed only in the direction of relative motion.

    Length contraction was first proposed by physicists G. F. Fitzgerald and, independently, Hendrick A. Lorentz as a explanation of why experiments such as those of Fizeau (who first measured the speed of light in the laboratory) and Michelson and Morley failed to detect any change in the Speed of Light no matter which direction their detection apparatus and their laboratories were oriented relative to the cosmic motions of the earth.  Their theory of contraction in the direction of motion (in the form of the Lorentz Transformation and the Fitzgerald contraction) was adopted by Einstein who explained with SR why it worked.

    Mass Inflation

    Consider the bouncing basketball again.  In order to describe another prediction of SR we must introduce a new concept -- momentum.  Momentum is a measure of the energy of a moving object.  The momentum (p) of our bouncing ball is given by
     
    p = v m
    where v is its speed and m is its mass. In this case since the ball's speed is constantly changing as it traverses its arc and because the boy gives it a slight push each time it reaches the top of that arc it is also true that the ball's momentum is constantly changing.  So either we will have to speak of its average momentum or instantaneous momentum at some point in its flight or at least remember that that is what we mean even though we do not say so.
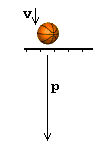    We are not moving with the boy and his ball so we observe them moving in the direction in which they are carried by the train.  The movement of the ball between the player's hand and the floor of the car therefore appears slower to us than it does to him and other observers that ride along with him on the train.  So when we compute the ball's momentum in this direction we come to the conclusion that it is less than that computed by observers riding on the train with the boy and his ball.
     

    		Since we also see the ball moving in concert with the train we compute its momentum in this direction as well.  Because of the length contraction we observe and described above the speed and therefore the additional momentum of the ball in this direction appears to us less than if there were no contraction.  When we add the two components of the ball's momentum together it is still less than that observed in the frame of reference of the moving car (shown here in red). 
    Since the ball cannot have two different momentums something must change to balance these results and in this case that something must be the mass of the ball -- which therefore appears to us to have increased!
     

    Mass and Energy

    There is an energy associated with motion.  It is called kinetic energy (Ek) and in pre-SR classical physics it is related to both the mass (m) of the moving object and its speed (v) as follows:
    Ek = 1/2 m v2
    We have just seen that the mass of an object increases with its speed.  Before SR mass was thought of as a constant.  A relativistic understanding of kinetic energy requires an adjustment for mass inflation.

    Not only does an object's mass increase with its speed, as the its speed approaches the Speed of Light (c) its mass approaches infinity.  The following expression shows how the relativistic mass of an object is related to its mass at rest or rest mass (m0) and the Speed of Light:

    m = m0 / ( 1 - v2 / c2 )
    Also in pre-SR classical physics the acceleration (a) an object experiences is related to its mass and the force (f) that is accelerating it:
    a = f / m
    Again pre-SR classical physics assumed mass was a fixed quantity and that unlimited acceleration was a possibility.  A relativistic understanding of acceleration says that as an object's speed increases its acceleration will slow unless a greater force can be applied.  No object can be accelerated to the speed of light because the force required to do so like its resulting mass would be infinite and infinite quantities of anything can't exist in the real world.

    The relativistic expression by which we calculate the mass of a moving object can further be reduced to:

    m = 1/2 m0 v2 / c2
    The first part of the expression to the right of the equal sign (1/2 m0 v2) is also the expression for kinetic energy so we will use e in its place in the last expression and rewrite it as:
    m = e / c2
    or, more famously:
    e = m c2
    The equivalence of mass and energy thus shown by SR solved a problem in classical physics.  In the late 19th century scientists had discovered radioactivity -- a phenomenon in which energy is released from certain elements seemingly without cause or effect.  This violated the principle of Conservation of Energy which was thought to be a law of nature.  According to this principle energy could neither be created or destroyed -- only transformed into other forms.  SR offered a solution to this conundrum since it shows that tiny amounts of mass can be converted into vast amounts of energy.  Physicists now knew to look for and found the tiny loss of mass that explained the source of the mysterious radiation.

    In solving the problem of radioactivity SR also superseded another long-standing physical principle -- Conservation of Mass.  Prior to SR it was also thought that mass like energy could not be created or destroyed -- only transformed into other forms.  SR essentially replaced these two conservation principles with a third -- Conservation of Mass and Energy.  Now in addition to other forms of energy we know that energy can be converted into mass.  And in addition to other forms of matter mass can be converted into energy.

    In addition to solving the problem of radioactivity SR provided an answer to the question of how the stars are powered.  It also showed us the possibility of both nuclear power and nuclear weapons.

    The equivalence of mass and energy is a consequence of the fact that by operating as a limit the Speed of Light enters in to the calculation of both mass and energy.

    Spacetime Diagrams

    Spacetime diagrams are another (mostly) non-mathematical way to explore SR.
     
     
    Rene Descartes invented a system of measuring positions in space known as the Cartesian co-ordinate system.  Any position can be expressed by 3 numbers in an arbitrary reference system.  The distance distance dAB between two points in space (A and B) can be easily calculated in this system because:
    dAB2 = dxAB2 + dyAB2 + dzAB2
    We can extend the concept of the Cartesian co-ordinate system by adding another scale -- time.  This is not easy to do in a diagram so we adjust by collapsing the 3 dimensions of space into one or 2 dimensions.  In 2 dimensions we use the horizontal scale to represent space and the vertical scale to represent time.  The result is a spacetime diagram.

    For units of measure to mark off the scale of our spacetime diagram we choose the Second for the time scale and the distance light travels in a second for the space scale. This has the convenient result that the Speed of Light is a 45o line through the origin. It also has the effect of emphasizing that there are comparable units of space and time. There are any number of units we can choose that are comparable in this way -- the hour and the light-hour, the year and the light-year, etc.  The choice is arbitrary and the diagram always looks and behaves the same no matter which comparable units we use.
     

    		If we draw a spacetime diagram for ourselves then the horizontal scale represents the three spacial dimensions.  Everything that we consider to be happening Now is on this line.  All events that we would call simultaneous must occur on this line or another parallel to it. The vertical line represents our past and future (depending on its intersection with space at what we call the Here and Now) and is called our worldline. 

    The area between the 45o Speed of Light lines and above the horizontal space axis is where we cannot go since this would involve exceeding the Speed of Light.  Similarly there is an area below the space axis where we can never have been.  I have labeled these areas that are beyond our reach "Elsewhere".
    All light that we see Here & Now whether it comes to us from the distant stars or the bulb across the room travels the diagonal paths on our spacetime diagram that border our past.  Any light or other electromagnetic emission we send forth travels in the opposite direction along those diagonal paths that border our future.  No signal can reach us in the Here & Now from Elsewhere.  No event in the Elsewhere can effect us in the Here & Now.  Neither can any signal or effect from us in the Here & Now effect any event in the Elsewhere.

    At some future time we will see events in our past that were then in our Elsewhere and conclude that they were simultaneous with our past Here and Now.  And at the same future time some events that will be simultaneous with our Here and Now will have been effected by our past Here and Now even though they will then be in our Elsewhere.
     
     
    Now we add a line to our spacetime diagram representing a traveler passing close by.  If they are in uniform motion relative to us their path is a worldline that crosses our spacetime at an angle defined by their speed.  This line is their time axis in their spacetime.  Given our chosen scales they have to be traveling pretty fast for us to find any significant deviation between our world line

     

    		Their spacetime diagram looks just like ours except that they see us moving in the opposite direction.  Since our world lines are tilted with respect to each other's and we know that for each of us space is perpendicular to our worldline in our own spacetime we can conclude that our passerby's definition of space is not the same as ours. 
    Therefore since the space axis of each of our spacetimes defines what is simultaneous to us we can conclude that we will not agree on which events are simultaneous (as we have previously seen).  As a corollary we can also conclude that some events which are concurrent with our Here and Now may be in our passerby's future and others in their past.  They can conclude the same about us.

    To complete the picture of how our passerby's spacetime is different than ours we will need more development of the concept of spacetime coordinates.  In Cartesian space two observers can always agree on the distance between two points (their space interval) so long as they use the same units of measure.  They do not have to use the same coordinate system.  So where a second observer measures the position of the same two points (A and B) from above in ' (prime) coordinates:

    dx'AB2 + dy'AB2 + dz'AB2 = dxAB2 + dyAB2 + dzAB2
    I.e., the space interval between any two points in Cartesian space is invariant with regard to the coordinate system used to measure it.

    Since we constructed our spacetime diagram by simply adding a time dimension to the three space dimensions we might naively assume that we can measure spacetime intervals (iAB) in a manner similar to the way we measure space intervals in Cartesian coordinates:

    iAB2 = dtAB2 + dsAB2
    (Note that we have simplified the space dimensions in this expression by dsAB2 =dxAB2 + dyAB2 + dzAB2 and that the result more closely matches our spacetime diagrams.)

    However SR says that this is not how spacetime is structured.  Instead spacetime intervals are calculated as follows:

    iAB2 = dtAB2 - dsAB2
    The minus sign in place of the plus sign in this expression is counter to our common sense and accounts for all the odd properties SR ascribes to spacetime.  Spacetime intervals are invariant no matter what the relative position and motion of observers:
    dt'AB2 - ds'AB2 = dtAB2 - dsAB2
    And the spacetime interval between any two events located on the Speed of Light diagonal on our spacetime diagrams is 0 (zero).
     
    The expression for the spacetime interval is also the formula for a hyperbola.  In fact it is the formula for a spacetime hyper hyperbola with an infinite number of solutions.  If we choose an interval equal to 1 (one) however we get just one solution which we add to our space time diagram.  We also add the worldline of a passerby who passes through our Here and Now.  Choosing their path in this way will clarify what we see.
    The significance of the hyperbola in this diagram is that it is the surface of all points in spacetime whose distance from Here and Now is 1 (one).  Therefore where our passerby's path intersects this hyperbola is where their time is 1.  Inspection of the diagram shows that the faster a passerby moves the more a unit of their time increases.  This is time dilation
    The hyperbola in our diagram occupies the time-like portion of our spacetime diagram and therefore is called the time-like spacetime interval.  Another similar expression can be used to derive corresponding space-like spacetime intervals:
    iAB2 = dsAB2 - dtAB2

    		 We add it to our spacetime diagram along with a space axis for our passerby.  Their space axis is shifted because they like we agree on the Speed of Light.  And the Speed of Light is by definition a line equidistance between the time and space axis's of a spacetime diagram.  Finally this particular spacetime diagram represents spacetime from our perspective -- for which the Speed of Light is already defined.

    As in the previous diagram the hyperbola is the surface of all points in spacetime whose distance from Here and Now is 1 (one).  Therefore where our passerby's space axis intersects this hyperbola is where their space interval is 1.  Since this point is in our Elsewhere we have to wait until light from there can reach us before we can measure it.  What we observe is that light takes less time to reach us (at ts') from where their space interval is 1 than it does (at ts) from a point where our space interval is 1.  We conclude that in our spacetime their space interval of 1 is smaller than ours.  This is length contraction.
     
     

    Note on graphics

    Please note that the train graphics are offered only to assist in visualizing the discussion and add to the visual appeal of the page.  Specifically it should be noted that they are not to scale in time.  At full speed a train would be moving more than 10 times the speed of the ball and therefore the down track distance the ball travels on each bounce should be 10 times the height of the bounce.  Light on the other hand travels about 100 million times faster than the ball so the down track distance on each bounce of the light beam should be 10 million times smaller.  To produce comprehensible graphics it was therefore necessary to adjust time and space in each.

    Note on the spacetime interval

    The expression for the space time interval can be derived from the Lorentz Transformation or Fitzgerald contraction developed, respectively, by physicists Hendrick A. Lorentz and G. F. Fitzgerald to explain the negative result of the Michelson-Morley experiment.  So this seemingly mysterious equation is simply an observed fact discovered by experiment and given mathematical expression.

     Top | Relative Motion | The Speed of Light Constant | Time Dilation | Simultaneity | Length Contraction
    Mass Inflation | Mass and Energy | Spacetime Diagrams


    Home.Return to Tom Jonard's Relativity page.
    Created June 19, 2002, 
    © 2002, Thomas A. Jonard